EVAP1

Termodinámica

Leyes de la Termodinámica

Primera ley de la termodinámica

También conocida como principio de conservación de la energía para la termodinámica, establece que si se realiza trabajo sobre un sistema o bien este intercambia calor con otro, la energía interna del sistema cambiará.

Visto de otra forma, esta ley permite definir el calor como la energía necesaria que debe intercambiar el sistema para compensar las diferencias entre trabajo y energía interna.

Fue propuesta por Nicolas Léonard Sadi Carnot en 1824, en su obra Reflexiones sobre la potencia motriz del fuego y sobre las máquinas adecuadas para desarrollar esta potencia, en la que expuso los dos primeros principios de la termodinámica. Esta obra fue incomprendida por los científicos de su época, y más tarde fue utilizada por Rudolf Clausius y Lord Kelvin para formular, de una manera matemática, las bases de la termodinámica.

Que aplicada a la termodinámica teniendo en cuenta el criterio de signos termodinámico, queda de la forma.

Donde U es la energía interna del sistema (aislado), Q es la cantidad de calor aportado al sistema y W es el trabajo realizado por el sistema.

 Esta última expresión es igual de frecuente encontrarla en la forma.

Ambas expresiones, aparentemente contradictorias, son correctas y su diferencia está en que se aplique el convenio de signos IUPAC o el Tradicional.

Segunda ley de la termodinámica

Esta ley marca la dirección en la que deben llevarse a cabo los procesos termodinámicos y, por lo tanto, la imposibilidad de que ocurran en el sentido contrario (por ejemplo, dice algo así como que una mancha de tinta dispersada en el agua no puede volver a concentrarse en un pequeño volumen). También establece, en algunos casos, la imposibilidad de convertir completamente toda la energía de un tipo a otro sin pérdidas. De esta forma, la segunda ley impone restricciones para las transferencias de energía que hipotéticamente pudieran llevarse a cabo teniendo en cuenta solo el primer principio. Esta ley apoya todo su contenido aceptando la existencia de una magnitud física llamada entropía, de tal manera que, para un sistema aislado (que no intercambia materia ni energía con su entorno), la variación de la entropía siempre debe ser mayor que cero.

Debido a esta ley también se tiene que el flujo espontáneo de calor siempre es unidireccional, desde los cuerpos de mayor temperatura hacia los de menor temperatura, hasta lograr un equilibrio térmico.

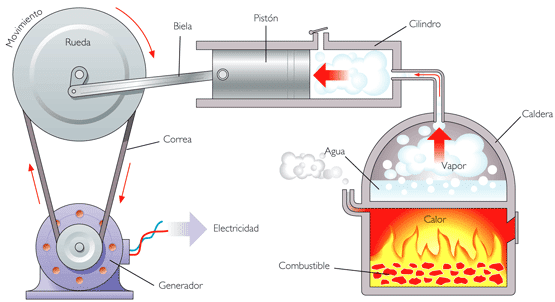
La aplicación más conocida es la de las máquinas térmicas, que obtienen trabajo mecánico mediante aporte de calor de una fuente o foco caliente, para ceder parte de este calor a la fuente o foco o sumidero frío. La diferencia entre los dos calores tiene su equivalente en el trabajo mecánico obtenido.

Solución de problemas

1.- ¿Cuál es el incremento en la energía interna de un sistema si se le suministran 700 calorías de calor y se le aplica un trabajo de 900 Joules?

Solución: El problema indica que se le están suministrando 700 calorías de calor, eso quiere decir que será positivo, por otra parte nos dice que al sistema se le aplicará un trabajo de 900 Joules, aquí el signo de  tendrá que ser negativo, puesto que se la están aplicando al sistema.

Sabiendo ese análisis podemos dar solución al problema de la siguiente forma:

Vamos a convertir las 700 calorías de calor en Joules.

Recordar que  porque como dijimos, al sistema se le está aplicando un trabajo. Ahora conforme a la fórmula de la primera ley de la termodinámica, iniciemos a sustituir.

despejando ” “

Sustituyendo

Diagrama de flujo y algoritmo

Inicio

¿Cuál es el incremento en la energía interna de un sistema si se le suministran 700 calorías de calor y se le aplica un trabajo de 900 Joules?

Declaración

Q, w  ←Enteros

∆U ←Reales

Asignación

Q←2940J

W←900J

Proceso

∆Q=∆u+∆w

Resultado

∆u=3840J

Fin del algoritmo

Segundo problema

¿Cuál es la eficiencia de una máquina térmica a la cual se le suministrarán 8 000 calorías para obtener 25 200 Joules de calor de salida?

Solución: Simplemente tenemos que sustituir los datos en nuestra fórmula:

  e =  (Q1 - Q2)/Q1

Sustituyendo nuestros datos:

e =  (8000cal – 6000cal)/8000cal

Lo que sería equivalente a un 25% de eficiencia térmica.

Diagrama de flujo y algoritmo

Inicio

¿Cuál es la eficiencia de una máquina térmica a la cual se le suministrarán 8 000 calorías para obtener 25 200 Joules de calor de salida?

Declaración

Q1, Q2←Enteros

 e ←Reales

Asignación

Q1←8000cal

Q2←6000cal

Proceso

e =  (Q1 - Q2)/Q1

Resultado

e=0.25

Fin del algoritmo